Example 1:
The delta function is defined by … . At the same time, one can show that no such function exists! Assume f, g \in L^2 to be equal almost everywhere — except for at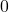 . Then, it is implied that (*)
. Then, it is implied that (*) 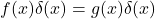 almost everywhere, and from this
almost everywhere, and from this 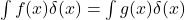 , which however (**) directly implies f(0) = g(0) — in contradiction with the initial assumption on f and g to be unequal at 0.
, which however (**) directly implies f(0) = g(0) — in contradiction with the initial assumption on f and g to be unequal at 0.
The inference to (**) involves a change of usage of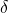 from occurring to an integral to not occurring in an intergral (and (*) such an inference in the opposite direction). According to Carney, physics practice simply does without inferences of type (*) and (**) with the effect tha contradiction as the one mentioned here are evaded.
from occurring to an integral to not occurring in an intergral (and (*) such an inference in the opposite direction). According to Carney, physics practice simply does without inferences of type (*) and (**) with the effect tha contradiction as the one mentioned here are evaded.
Example 2:
The path integral formalism is defined by … . At the same time, such a measure is only known in the Euclidean case (via the Wiener measure). According to Carney, physics practice can simply use the path integral as a generator of physical more well-defined expressions (such as for perturbation theory). Another way he mentions how one can use the formalism to derive the Schrödinger equation.
The important distinction is surely that between conservative, moderate and liberal … expand on this
The delta function is defined by … . At the same time, one can show that no such function exists! Assume f, g \in L^2 to be equal almost everywhere — except for at
The inference to (**) involves a change of usage of
Example 2:
The path integral formalism is defined by … . At the same time, such a measure is only known in the Euclidean case (via the Wiener measure). According to Carney, physics practice can simply use the path integral as a generator of physical more well-defined expressions (such as for perturbation theory). Another way he mentions how one can use the formalism to derive the Schrödinger equation.
The important distinction is surely that between conservative, moderate and liberal … expand on this